Математика - это просто!

ПЛОСКИЕ ФИГУРЫ

· Отрезок, луч, прямая
· Угол
· Разновидности углов
· Признаки параллельности

МНОГОУГОЛЬНИКИ

· Виды треугольников
· Биссектриса и высота
· Признаки равенства треугольников
· Равнобедренные треугольники
· Площадь треугольника
· Теорема Пифагора
· Теорема синусов
· Теорема косинусов
· Подобные треугольники
· Параллелограмм
· Ромб, квадрат
· Трапеция

ОКРУЖНОСТЬ и КРУГ

· Что такое окружность
· Что такое круг
· Касательная к окружности
· Вписанная окружность
· Описанная окружность

ВЕКТОРЫ

· Что такое вектор
· Сложение и вычитание векторов
· Умножение вектора на число
· Координаторы вектора
· Угол между векторами
· Скалярное произведение векторов

НАТУРАЛЬНЫЕ ЧИСЛА

ДРОБИ

УРАВНЕНИЯ и ТОЖДЕСТВА

ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ

ФУНКЦИИ

ТРИГОНОМЕТРИЯ

ВЫСШАЯ МАТЕМАТИКА

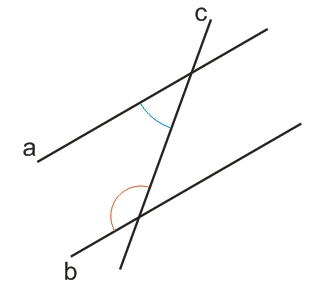
Признаки параллельности прямых

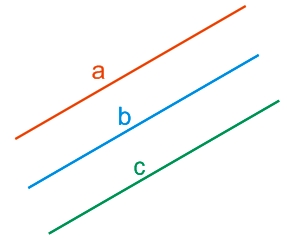
Признак 1. Если каждая из двух прямых a и b параллельна третьей прямой c, то такие прямые (a и b) параллельны между собой.

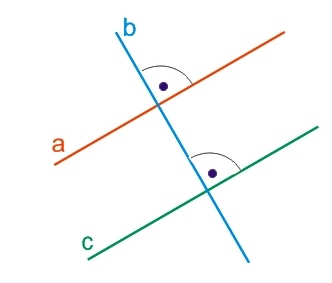
Признак 2. Если каждая из двух прямых a и с перпендикулярна третьей прямой b, то такие прямые (a и с) параллельны между собой.

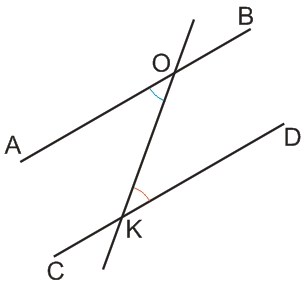
Признак 3. Если при пересечении двух прямых секущей образовавшиеся накрест лежащие углы равны между собой (∠AOK = ∠OKD) - такие прямые параллельны.

Признак 4. Если при пересечении двух прямых секущей образовавшиеся соответственные углы равны между собой (∠LOB = ∠LKD) - такие прямые параллельны.

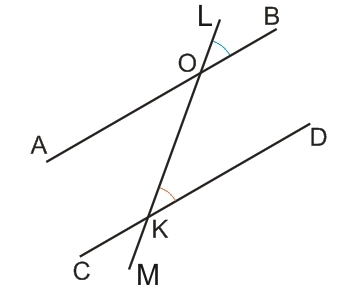
Признак 5. Если при пересечении двух прямых секущей сумма любой пары односторонних углов равна 180° - такие прямые параллельны.