Математика - это просто!

МНОГОУГОЛЬНИКИ

· Виды треугольников
· Биссектриса и высота
· Признаки равенства треугольников
· Равнобедренные треугольники
· Площадь треугольника
· Теорема Пифагора
· Теорема синусов
· Теорема косинусов
· Подобные треугольники
· Параллелограмм
· Ромб, квадрат
· Трапеция

ПЛОСКИЕ ФИГУРЫ

· Отрезок, луч, прямая
· Угол
· Разновидности углов
· Признаки параллельности

ОКРУЖНОСТЬ и КРУГ

· Что такое окружность
· Что такое круг
· Касательная к окружности
· Вписанная окружность
· Описанная окружность

ВЕКТОРЫ

· Что такое вектор
· Сложение и вычитание векторов
· Умножение вектора на число
· Координаторы вектора
· Угол между векторами
· Скалярное произведение векторов

НАТУРАЛЬНЫЕ ЧИСЛА

ДРОБИ

УРАВНЕНИЯ и ТОЖДЕСТВА

ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ

ФУНКЦИИ

ТРИГОНОМЕТРИЯ

ВЫСШАЯ МАТЕМАТИКА

Признаки равенства треугольников

Два треугольника считаются равными, если при их совмещении они полностью совпадают.

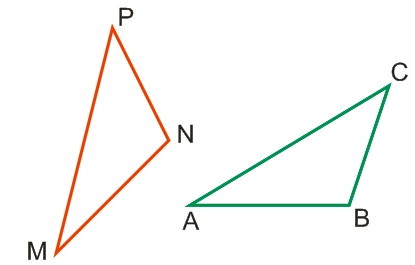
На рисунке треугольник АВС является точной копией треугольника MNP, повернутого на 45° по часовой стрелке.

Два треугольника будут равны, если:

1. имеется пара равных сторон с прилежащими к ним углами:
   
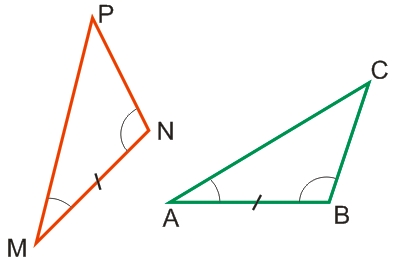
   • MN = AB;
   • (∠M) = (∠A);
   • (∠N) = (∠B).
   
   
2. имеется две пары равных сторон и равный угол, который заключен между этими сторонами:
   
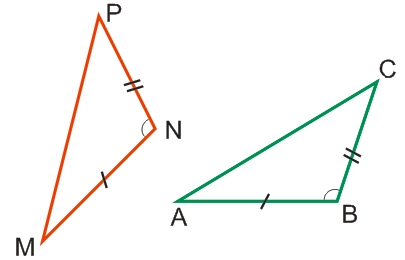
   • MN = AB;
   • NP = BC;
   • (∠N) = (∠B).
   
   
3. имеется три пары равных сторон:
   
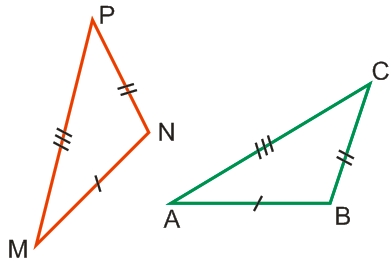
   • MN = AB
   • NP = BC
   • PM = CA

Еще одним частным случаем является равенство прямоугольных треугольников, у которых равны гипотенузы + одна из двух пар катетов. В этом случае будет равна и вторая пара катетов, поскольку квадрат гипотенузы равен сумме квадратов катетов. Таким образом, в таком прямоугольном треугольнике будут равны все стороны + один угол (прямой), и такой треугольник подпадает под второй пункт (см. выше).