Скалярное произведение векторов
Вектор можно не только умножать на число, но и перемножать вектора между собой. Такое действие носит название скалярного произведения векторов.
Если сложение или вычитание векторов является, в общем-то, достаточно понятным и логичным действием, которое просто отображается графически, то с пониманием скалярного произведения векторов не всё так просто. Гораздо легче запомнить формулу скалярного умножения двух векторов, благо, она куда проще для запоминания, нежели для понимания.
a·b=|a|·|b|·cos(∠ab)
- скалярное произведение перпендикулярных векторов равно нулю, т.к., cos(90°)=0;
- если хотя бы один из перемножаемых векторов является нулевым, то скалярное произведение также будет равно нулю;
- если ни один из перемножаемых векторов не является нулевым, а скалярное произведение векторов равно нулю, то угол между такими векторами будет прямым;
- если угол между векторами тупой, то скалярное произведение таких векторов будет отрицательным числом;
- если угол между векторами острый, то скалярное произведение таких векторов будет положительным числом;
- произведение вектора на самого себя будет равно квадрату модуля этого вектора.
Все же попробуем разъяснить суть умножения двух векторов.
Начнем с самого простого случая, когда два перемножаемых между собой вектора являются сонаправленными, т. е., угол между такими векторами будет равен 0°.
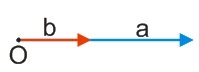
В таком случае:
a·b=|a|·|b|·cos(0°)=|a|·|b|
Таким образом, произведение сонаправленных векторов будет равно произведению их модулей, т.е., умножается длина одного вектора на длину второго вектора.
ВАЖНО: Обратите внимание, что результатом скалярного произведения векторов будет число, а не вектор!
А как быть, если перемножаемые между собой вектора расположены под некоторым углом друг к другу?
В этом случае в дело вступает косинус величины угла, под которым располагаются друг к другу перемножаемые вектора.
Возьмём ещё один частный случай, когда два вектора расположены перпендикулярно друг к другу, т.е. образуют угол в 90°.
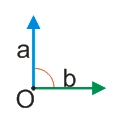
a·b=|a|·|b|·cos(90°)=|a|·|b|·0=0
Как видим, произведение двух перпендикулярых векторов равно 0.
Почему так происходит?
Нюанс перемножения двух векторов, расположенных друг к другу под некоторым углом, заключается в том, что перемножается модуль первого вектора на модуль проекции на этот вектор второго вектора. В случае перпендикулярности проекция второго вектора на первый будет являться точкой или нулевым вектором, а скалярное произведение вектора на нулевой вектор равно нулю (см. выше).
Возьмём третий возможный случай, когда угол между векторами острый, т.е., лежит в пределах от 0° до 90°.
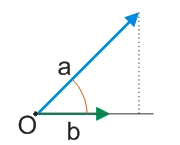
Как известно, косинус углов в этом диапазоне будет числом положительным - меньше 1, но больше 0. Поэтому, скалярное произведение двух не нулевых векторов, расположенных друг к другу под острым углом, всегда будет числом положительным (не следует забывать, что модуль вектора не может быть числом отрицательным, поскольку это расстояние между двумя точками).
В случае, если угол между перемножаемыми векторами будет тупой, т.е., больше 90°, но меньше 180°, в таком случае произведение таких векторов будет числом отрицательным, поскольку в этом диапазоне косинус колеблется от 0 до -1.
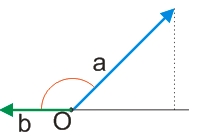
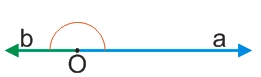
И последний частный возможный случай - перемножаемые вектора являются противопложно направленными, т.е., образуют развернутый угол (180°). В таком случае, поскольку cos(180°)=-1, скалярное произведение противоположно направленных векторов будет равно отрицательному произведению их модулей.
a·b=|a|·|b|·cos(180°)=-1·|a|·|b|
Скалярное произведение векторов, заданных координатами
Если:
- {x1;y1} координаты вектора a;
- {x2;y2} координаты вектора b;
- то: a·b = x1x2 + y1y2
Формула для вычисления длины вектора а с координатами {x;y}:
|a|=√(x2+y2)
Свойства скалярного произведения векторов:
- переместительный закон: ab = ba;
- распределительный закон: (a+b)c = ac+bc;
- сочетательный закон: (ka)b = k(ab), где k - любое число;
- отрицательный квадрат не нулевого вектора будет положительным числом: а-2>0.
