Что такое угол
Прямая делит плоскость, в которой она находится, на две полуплоскости, при этом считается, что сама прямая принадлежит обеим полуплоскостям.
Два луча, имеющих общее начало, также делят плоскость на две части, каждая из которых называется углом, при этом точка, из которой выходят лучи, называется вершиной угла.

В этом месте следует обратить внимание читателя на весьма важный момент.
Чтобы было понятнее, проведем аналогию с окружностью и кругом:
- Окружность - это сама линия, которая ограничивает некую часть плоскости;
- Круг - это часть плоскости, ограниченная окружностью, т.е., то, что находится внутри окружности.
Аналогично и с углом, только с той лишь разницей, что углом называют, как непосредственно два луча, имеющих общее начало, так и плоскости, ограниченные линиями лучей.
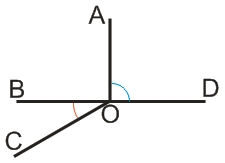
В случае, если два луча выходят из одной точки и идут в противоположных направлениях, то они образуют два развернутых угла (по 180° каждый). В противном случае, один из углов будет меньше развернутого (синий сектор на рисунке выше), а второй угол - больше развернутого (красный сектор).
Оба угла, образуемых лучами, носят одинаковое название (на рисунке - АОС), при этом буква, обозначающая точку начала лучей, ставится между буквами, обозначающими точки на каждом луче.
Если речь идет о двух углах, один из которых меньше развернутого, а другой - больше, то считается что рассматривается меньший угол, если это специально не оговорено (на рисунке выделен синим сектором).
Если оба угла являются развернутыми, то рассматриваться может любой из углов.
Если угол привязывается к тригонометрическим функциям, то положительным углом считается угол, полученный вращением луча Ох, против часовой стрелки, и, наоборот, угол, полученный вращением луча Ох по часовой стрелке - считается отрицательным. Например, если луч Ох сделал одну четверть оборота против часовой стрелки, мы получим угол π/2 (или 90°). И, наоборот, угол, равный -2π, был получен вращением луча Ох на полный оборот по часовой стрелке.
Биссектриса угла
Любой луч, начало которого совпадает с вершиной развернутого угла, делит этот угол на два угла.
Любой луч, начало которого совпадает с вершиной не развернутого угла, и при этом такой луч проходит внутри угла, делит не развернутый угол на два угла.
Биссектрисой называется луч, который делит угол на два равных угла.

Луч ОВ является биссектрисой угла АОС, который больше развернутого(красный сектор). Луч OD является биссектрисой угла АОС, который меньше развернутого (синий сектор).
Смежные углы
Смежными называются углы, имеющие одну общую сторону, при этом две другие их стороны образуют развернутый угол.
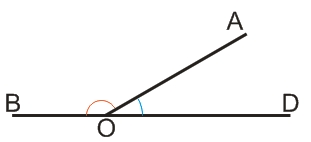
Сумма смежных углов равна 180°.
Углы АОС (красный сектор) и AOD (синий сектор) на рисунке ниже, не являются смежными, т.к. они имеют одну общую сторону, но две их оставшиеся стороны не образуют развернутый угол.
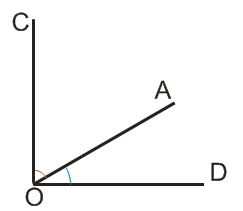
Углы COB (красный сектор) и AOD (синий сектор) на рисунке ниже, не являются смежными, т.к., не имеют общей стороны.
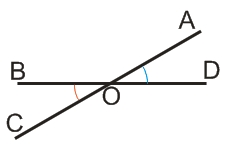
Вертикальные углы
Два угла называются вертикальными, если одна и вторая пара их сторон образуют развернутые углы.

Вертикальные углы равны между собой.
Углы COB (красный сектор) и AOD (синий сектор) на рисунке ниже, не являются вертикальными, т.к., вторая пара их сторон не образуют развернутого угла.