Координаты вектора
Любой не нулевой вектор a можно выразить через не коллинеарные единичные координатные векторы i, j:
a = xi+yj
Поскольку речь зашла о координатных векторах, то не обойтись без прямоугольной системы координат.
Направление единичного координатного вектора i (изображен голубым цветом на рисунке ниже) совпадает с положительным направлением оси абсцисс; вектора j (красный цвет) - с положительным направлением оси ординат, при этом |i|=|j|=1:
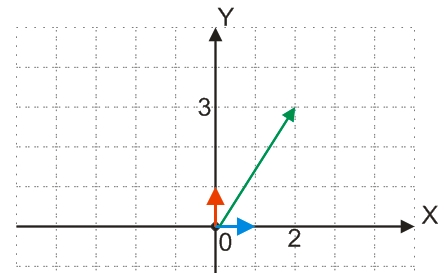
Любой вектор a в прямоугольной системе координат с координатными векторами i и j, характеризуется абсциссой (x) и ординатой (y), где x и y - числа в разложении вектора a по векторам i и j.
На рисунке выше вектор (зеленый цвет) имеет координаты (2;3) и может быть разложен через координатные векторы:
a = 2i+3j
Равные векторы всегда имеют одни и те же координаты.
При сложении векторов их координаты складываются:
a{x1;y1}
b{x2;y2}
c=a+b
c{x1+x2;y1+y2}
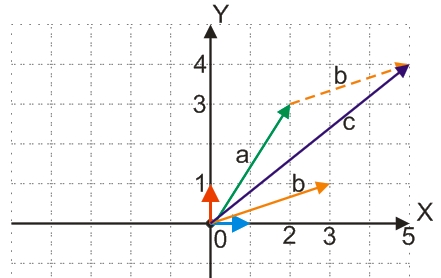
Рассмотрим пример сложения векторов a{2;3} и b{3;1}, изображенный на рисунке выше:
c=a+b
c{2+3;3+1}=с{5;4}
Если провести графические построения, то из рисунка видно, что коррдинаты результирующего вектора с{5;4}, что совпадает с вычисленными по формуле.
При вычитании векторов их координаты вычитаются:
a{x1;y1}
b{x2;y2}
c=a-b; c=a+(-b)
c{x1+(-x2);y1+(-y2)}
Произведение вектора a{x;y} на число k будет вектор с координатами {kx;ky}.
